Bài viết này được thực hiện khi tôi đang học học phần Cấu trúc dữ liệu và giải thuật và Lí thuyết đồ thị của kì 2, năm 2 (2018-2019). Trong quá trình học môn học, tôi thấy Disjoint Set Union là một cấu trúc dữ liệu rất hữu ích cho các bài toán xử lí trên đồ thị. Khi muốn duyệt hay quản lí các đỉnh trong đồ thị mà có nhiều thành phần rời rạc nhau thì DSU là một lựa chọn tối ưu và nhanh vì ta không phải duyệt lại toàn bộ đồ thị với DFS / BFS.

Disjoint Set Union là gì?

Nói qua về DSU. Có một tập các phần tử, mỗi phần tử trong số đó là một tập riêng biệt. Một DSU sẽ có 1 thao tác gộp 2 tập bất kỳ thành 1 tập lớn hơn, và có thể chỉ ra được 1 phần tử cụ thể nằm trong tập nào.

Về cơ bản, DSU gồm 3 thao tác chính:

• make_set(v) – tạo ra một tập mới gồm phần tử mới là v
• Union(a, b) – gộp 2 tập riêng biệt chứa 2 nút a và b. Nếu a và b cùng một tập thì không làm gì cả
• Find(v) – trả về nút gốc (nhãn) của tập chứa phần tử v. Nhãn này là 1 phần tử của tập tương ứng với nó. Nhãn này có thể được sử dụng để kiểm tra xem liệu 2 phần tử có cùng nằm trong 1 tập hay không. Nếu find_set(a) == find_set(b) thì a và b sẽ cùng 1 tập và ngược lại.

Cách cài đặt

Bản đơn giản

Ban đầu chúng ta có thể viết ngay được bản implement cho DSU. Tuy nhiên nó tỏ ra không hiệu quả, chúng ta có thể cải thiện điều này sau với một vài thao tác tối ưu, do đó thời gian gọi hàm sẽ gần là tuyến tính.

Như chúng ta đã nói, mọi thông tin về các tập hợp của các phần tử đều được lưu trong mảng parent.

Để tạo ra một tập mới (thao tác make_set(v)), đơn giản chúng ta chỉ cần tạo 1 cây với gốc là đỉnh v, nghĩa là v là tổ tiên của chính nó.

Để gộp 2 tập (thao tác Union(a, b)), ban đầu ta sẽ tìm gốc (nhãn) của tập chứa nút a, và gốc của tập chứa nút b. Nếu a và b cùng gốc hay cùng nằm trong 1 tập thì hiển nhiên chúng ta không cần gộp làm gì cả, 2 tập đã được gộp sẵn. Ngược lại, đơn giản chúng ta xác định 1 gốc là cha của gốc còn lại, bằng cách đó ta kết hợp 2 cây.

Cuối cùng là hàm dùng để tìm gốc (thao tác Find(v)): đơn giản chúng ta “leo” trên cây để tìm ra tổ tiên của đỉnh v hay hiểu là tìm gốc của tập chứa v cho đến khi gặp gốc. Một đỉnh có thể chính nó là tổ tiên (gốc).. Thao tác này được chạy bằng đệ quy.

Tuy nhiên, như đã nói, bản cài đặt này không hiệu quả, dễ hiểu nếu ta gộp cây lớn hơn vào cây nhỏ hơn.

Trường hợp này mỗi lần gọi hàm Find(v) có thể mất O(n). Nhưng độ phức tạp mà chúng ta muốn là gần tuyến tính. Do đó ta cân nhắc 2 phương pháp tối ưu là Nén đường đi và Gộp dựa trên kích cỡ / độ sâu của cây.

Nén đường đi (Path compression optimization)

Phương pháp tối ưu này được thiết kế để tăng tốc hàm Find.

Nếu ta gọi hàm Find(v) cho đỉnh v nào đó, ta sẽ tìm gốc p cho mọi nút (đỉnh) mà chúng ta đi qua trên quãng đường tới đỉnh gốc p thật. Mẹo ở đây đó là rút ngắn các đường đi cho tất cả nút, bằng cách đặt nút cha của các nút đã đi qua trực tiếp là nút con của nút gốc p.

Có thể hình dung thao tác đó qua ảnh dưới đây. Bên trái là 1 cây. Bên phải là 1 cây đã được nén đường đi sau khi gọi hàm Find(7), điều này giúp rút đường đi cho các nút đã đi qua 7, 5, 3 và 2.

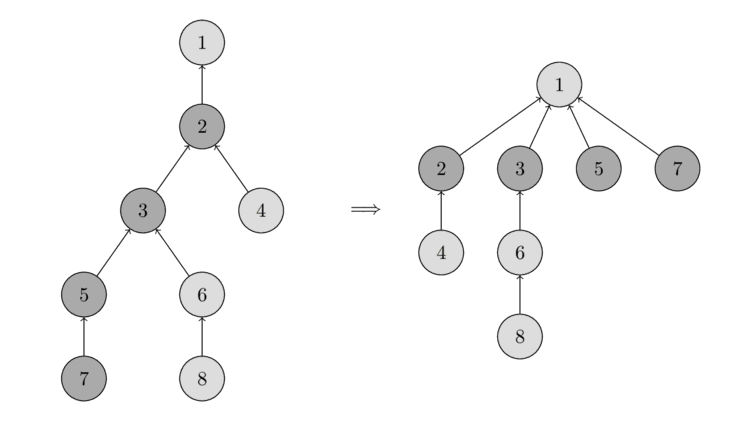
Bản cày đặt mới cho hàm Find như sau:

// path compression 
int Find(int v){ 
    if(par[v] != v) par[v] = Find(par[v]); 
    return par[v]; 
} 

Kĩ thuật nén đường đi này có thể đạt được độ phức tạp thời gian trung bình chỉ còn O(logn) mỗi lần gọi.

Gộp dựa trên kích cỡ / độ sâu của cây (Union by size / rank)

Phương pháp tối ưu này để thay đổi thao tác Union. Chính xác là ta sẽ thay đổi cây nào sẽ được gộp vào cây còn lại. Ở bản cài đặt đơn giản, ta luôn luôn gộp vào cây thứ nhất. Thực tế điều này có thể dẫn tới độ phức tạp O(n). Trong phương pháp này ta sẽ tránh được điều đó bằng cách chọn cây nào được gộp vào cây nào một cách rất cẩn thận.

Có nhiều phương pháp heuristics được sử dụng. Hai phương pháp phổ biến nhất đó là ưu tiên kích cỡ của cây và ưu tiên độ sâu của cây (hay chính xác hơn là cận trên độ sâu của cây vì độ sâu của cây sẽ nhỏ đi khi ta dùng them kĩ thuật nén đường đi đã được trình bày trước đó).

Hiệu quả của 2 phương pháp này là như nhau: ta gán cây có bậc thấp hơn cho cây có bậc cao hơn.

Đây là bản cài đặt cho phương pháp gộp dựa trên kích cỡ (Union by size):

// union by size 
void make_set(int v){ 
    par[v] = -1; 
} 
int Find(int v){ 
    return par[v] < 0 ? v : par[v] = Find(par[v]); 
} 
void Union(int a, int b){ 
    if((a = Find(a)) == (b = Find(b))) return; 
    if(par[b] < par[a]) swap(a,b); 
    par[a] += par[b]; 
    par[b] = a; 
} 

Và đây là bản cài đặt cho phương pháp gộp dựa trên độ sâu (Union by depth):

/// union by depth
  
void make_set(int v){
    par[v] = v;
    Rank[v] = 0;
}
int Find(int v){
    if(par[v] != v) par[v] = Find(par[v]);
    return par[v];
}
void Union(int a, int b){
    int x = Find(a); int y = Find(b);
    if(x == y) return;
    if(Rank[x] == Rank[y]) Rank[x]++;
    if(Rank[x] < Rank[y]) par[u] = v;
    else par[v] = u;
}

Cả hai đều có độ phức tạp thời gian cũng như bộ nhớ tương đương nhau.

Độ phức tạp (Complexity)

Như đã đề cập bên trên, nếu chúng ta kết hợp cả nén đường đi và gộp dựa trên size / rank chúng ta sẽ gần đạt thời gian tuyến tính. Do đó độ phức tạp thời gian tổng thể sẽ rơi vào O(α(n)) với α(n) là nghịch đảo hàm Ackermann với độ tang rất chậm, người ta chứng minh được hàm này sẽ không thể vượt qua 4 với mọi n đủ lớn (n < 10^600).